V jednom z minulých čísel REVI byl uveden článek „Neuvěřitelný příběh palubního střelce“ popisující jeden zajímavý letecký příběh z 2. světové války nad Mandžuskem, což je oblast na severovýchodě dnešní Číny (REVI č. 50, str. 4). Autor v něm zmiňuje, že ve výšce 6,5 km byla teplota -68º F (Fahrenheita) odpovídající -55° C, což se některým našim čtenářům zdálo neuvěřitelné. Pokusíme se objasnit, proč a jakým způsobem se teplota s rostoucí výškou mění a zda je vůbec možné, aby v uvedené výšce klesla teplota tak hluboko pod bod mrazu. 
   
   Atmosféra je velmi složitý systém. Jednotlivé meteorologické prvky, jako například tlak, teplota, vlhkost, apod. jsou prostorově velmi proměnlivé. Změny zaznamenáváme nejen v horizontální rovině, ale především po vertikále. A právě chování teploty se změnou výšky je předmětem tohoto článku.
   Uvažujme určitou omezenou oblast atmosféry, pro lepší představu ji budeme nazývat vzduchovou bublinou, což je jistě přirozenější (lidštější) pojmenování. Navíc „omezená oblast atmosféry“ může být stále ještě velmi rozsáhlá, kdežto vzduchovou bublinu chápeme spíše jako prostorově ne příliš rozsáhlý objekt, což je výhodné, neboť v dalších úvahách budeme potřebovat, abychom naší bublině mohli přiřadit právě jednu meteorologickou veličinu (teplotu, tlak, vlhkost, atd.) v celém jejím objemu. Představme si nyní, že se zmíněnou bublinou vystoupíme do větší výšky. Co se stane? Určitě poklesne tlak. Tlak je totiž způsoben vlastní tíhou atmosféry, konkrétně tíhou sloupce nad uvažovaným místem. Při vzestupu bubliny se zmenší tíha sloupce nad ní a tlak tudíž poklesne. Při menším tlaku se bublina samozřejmě zvětší. A co se stane s teplotou? Na to bohužel ještě nejsme schopni odpovědět. Nejdřív je totiž třeba určit, jak se při vzestupu změnila celková energie naší bubliny a její jednotlivé druhy. K tomu použijeme 1. větu termodynamickou, která není ničím jiným, než zákonem zachování energie. Můžeme ji zapsat například následujícím způsobem




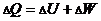
(1)



   Symbolem D dáváme najevo, že budeme počítat se změnami veličin. Písmenem U značíme vnitřní energii. Co si pod tímto pojmem představit? Plyn je složen z jednotlivých molekul, které se pohybují, mají tedy určitou kinetickou energii. Zároveň se molekuly ovlivňují mezi sebou navzájem, mají tedy i potenciální energii. Toto ovlivnění je při tlacích, které se v atmosféře běžně vyskytují velmi malé a často se zanedbává. Každá molekula má tedy svou celkovou energii, součet energií všech molekul se nazývá vnitřní energie. Lze si ji tedy představit jako energii, akumulovanou v daném plynu. DU tedy bude změna vnitřní energie. DQ znamená energii dodanou při zkoumaném procesu. Ač to není na první pohled zřejmé, jedná se také o změnu. Bublině byla jistě v minulosti dodána nějaká energie, kterou však nejsme schopni určit. Podaří se nám však určit energii, dodanou při příslušném procesu. Nebudeme tedy znát počáteční ani konečný úhrn energie, naštěstí však určíme jejich rozdíl, který vystupuje ve výše uvedené rovnici. DW je práce, kterou plyn při procesu vykonal.
   Popišme uvedenou rovnici slovy: Dodaná energie se spotřebuje na změnu vnitřní energie a práci, kterou plyn vykoná. V případě, že žádnou energii nedodáme (DQ = 0), bude práce, kterou by plyn případně vykonal, kompenzována snížením vnitřní energie, tedy energie akumulované v plynu. Procesy, při nichž nedochází k dodávání tepla (DQ = 0) jsou velmi významné a nazývají se adiabatické.
   Pro určení změny teploty bubliny při jejím vzestupu potřebujeme ještě rovnici hydrostatické rovnováhy

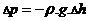
(2)

   Rovnice určuje, o kolik se změní tlak (Dp) při změně výšky (Dh). Písmeno r značí hustotu tekutiny (v našem případě je onou tekutinou vzduch) a g je tíhové zrychlení (g = 9,81m.s-2). Znaménko mínus značí, že tlak s rostoucí výškou klesá.
   Necháme tedy bublinu vystupovat. Budeme předpokládat, že se jedná o adiabatický děj (zanedbáme například ohřev od Slunce, od země). Při vzestupu bublina vykoná práci a sníží se její vnitřní energie. Jakého druhu bude práce, kterou bublina vykoná? Přesunuli jsme bublinu o Dh výše. V této výšce je vzduch, který má nižší tlak, než jaký byl původní tlak bubliny. Při svém rozpínání působí bublina proti tomuto nižšímu tlaku. Lze si tedy představit, že bublina působí silou proti pístu, na jehož opačné straně je příslušný nižší tlak a posune ho o určitou vzdálenost, čímž jsme dospěli ke klasické představě vykonané práce (síla působící po určité dráze).
   Přistupme k výpočtu. 1. větu termodynamickou lze vyjádřit též ve tvaru

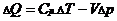
(3)

   kde Cp je konstanta, uvádějící kolik energie musíme dodat naší bublině, aby se ohřála o 1°C při stálém tlaku. T značí teplotu a V objem bubliny. Pro výpočet použijeme rovnici (3) pro adiabatický děj (DQ = 0) a rovnici (2). Naším cílem je určit změnu teploty příslušnou dané změně výšky, tedy

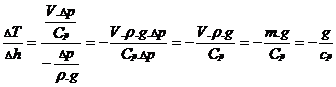
(4)

   kde cp uvádí, kolik energie musíme dodat 1kg vzduchu, aby se ohřál o 1° C při stálém tlaku. Tato hodnota je uvedena v tabulkách a pro suchý vzduch činní cp = 1007 J.kg-1.K-1. Po dosazení vyjde změna teploty přibližně 1º C na 100 m výšky. Mínus v rovnici (4) znamená, že teplota s výškou klesá.
   V předchozích úvahách jsme provedli jedno podstatné zjednodušení. Neuvažovali jsme totiž přítomnost vodní páry v atmosféře, což nyní napravíme. Nechť tedy naše bublina obsahuje vzduch a vodní páru. Předpokládejme, že vzduch je vodní parou nasycen. Při vzestupu bubliny klesne její teplota a tudíž část páry zkondenzuje. Abychom zjednodušili popis, předpokládejme, že zkondenzované kapky z bubliny ihned vypadávají a dále ji již neovlivňují. Právě popsaný proces se nazývá pseudoadiabatický. Při kondenzaci páry se uvolní takzvané latentní teplo a lze tedy očekávat, že pokles teploty bude pomalejší. A skutečně, vychází pokles pouze asi 0,6º C na 100 m výšky. Tato hodnota není pevná, závisí určitým způsobem na stavu bubliny. (Pro skalní fanoušky termodynamiky a jiné nadšence: Při odvození se vychází z rovnice pro latentní teplo, při úpravách je třeba uvažovat Clausius-Clapeyronovu rovnici.)
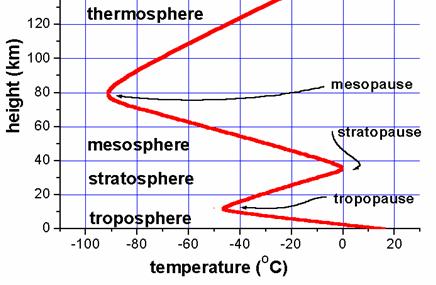
   Určili jsme tedy, jak (při uvedených zjednodušeních) klesá teplota s výškou. Klesá však tímto způsobem až na hranici atmosféry? Odpověď zní nikoli. Ve větších výškách se mění složení atmosféry, vstupují do hry i další procesy. Přibližný vertikální profil teploty je uveden na obrázku 1.
   V troposféře klesá teplota s výškou vlivem adiabatického rozpínání vzduchu, tedy podle principů, které jsme naznačili výše. Pro přesný profil by však bylo nutné zahrnout ještě další vlivy, například ohřev vzduchu a země vlivem slunečního záření, přenosy energie (DQ ¹ 0), atd.
   Ve stratosféře teplota s výškou roste. To je zapříčiněno především přítomností ozónu, který absorbuje ultrafialové záření, čímž se zahřívá.
   V mezosféře teplota klesá, není zde totiž dostatek ozónu pro absorbci ultrafialového záření.
   Teplota v termosféře je silně ovlivněna sluneční aktivitou a dosahuje až 2 000º C. Rozdíly mezi dnem a nocí se pohybují v řádu stovek stupňů. Nutno ovšem podotknout, že definovat teplotu v těchto výškách je poněkud obtížné, neboť vzduch je již natolik řídký, že klasické měřicí techniky nejsou praktické. Teplota se určuje například výpočtem z rychlosti pohybu molekul.

Obr. 1: Vertikální průběh teploty.

   Je zřejmé, že průběh teploty s výškou je poměrně komplikovaný a že i výpočet ostatních meteorologických veličin (tlak, hustota, atd.) v určité výšce by byl velmi náročný. Proto byla definována tzv. standardní atmosféra, která umožňuje meteorologické veličiny přibližně určit. Definice byla provedena pomocí změny teploty s výškou.

   Definice standardní atmosféry.

   Standardní tlak a teplota na hladině moře má hodnotu p0 = 1013,25 hPa a t0 = 15°C. Ostatní meteorologické veličiny byly určeny výpočtem a jsou uvedeny v tabulkách.

   Zkusme nyní odhadnout, jakou teplotu můžeme očekávat v zimních měsících nad Mandžuskem. Na obrázku 2 je vykresleno rozložení průměrné prosincové teploty v dané oblasti.

Obr.2: Průměrná prosincová teplota.

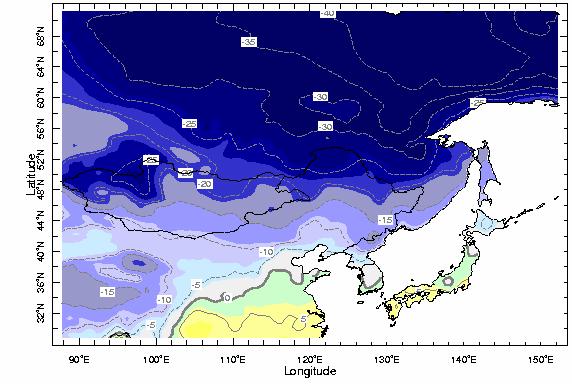
   Jak je vidět, tyto (ještě jednou zdůrazněme, že průměrné) teploty jsou velmi nízké. Co je toho příčinou? Voda má velkou měrnou tepelnou kapacitu (ono c v rovnici (4) ) a tudíž je třeba ji dodat značné množství energie, aby se zahřála. Stejně tak ovšem značné množství energie uvolní, když se bude ochlazovat. Tepelná kapacita pevniny je menší, a proto jsou změny teploty během roku na pevnině mnohem větší, než změny na moři. Evropa je v úzkém kontaktu s mořem, které ji v zimě ohřívá a v létě ochlazuje. Naproti tomu Asie je natolik rozsáhlým kontinentem, že v centrální části je vliv moří a oceánů minimální, a proto je v zimních měsících velmi studený. Naproti tomu v létě se poměrně dobře prohřeje. Největší změnu teploty během roku proto naměříme v centrální Asii, konkrétně v oblasti ruského Ojmjakonu a Verchojanska, což je zhruba oblast v horní části obrázku 2. Tato roční změna teploty může přesáhnout i 100º C. 
   Podle definice standardní atmosféry klesá teplota o 0,65º C na 100 m výšky, celkový pokles do výšky 6,5 km tedy činní přibližně 40º C. Jako typickou prosincovou přízemní teplotu v oblasti Mandžuska vezměme -15º C, s poklesem 40º C dospějeme k -55º C, které jsme zmínili v úvodu. Dlužno ještě podotknout, že velikost poklesu teploty nemusí být vždy taková, jaká je definována ve standardní atmosféře. Konkrétně v našem případě lze předpokládat, že profil teploty bude poněkud komplikovanější. Zemský povrch bude vyzařovat tepelné záření (podobně jako černé těleso), v důsledku čehož se tzv. radiačně ochladí. Pokles teploty s výškou pak bude pozvolnější, může dokonce nastat i situace, kdy teplota s výškou poroste (toto zvrstvení atmosféry se nazývá radiační inverze). Asijský kontinent, respektive atmosféra nad ním však bývá v zimě prochlazena do veliké výšky a za příznivých podmínek se nám jistě podaří naměřit ve výšce 6,5 km teplotu -55º C.